Rational Approximations for Complete Elliptic Integrals
Last modified:
Below is a list of rational approximations for complete elliptic integrals of the first and second kind. Higher order approximations are possible. Send questions to stefan at exstrom dot com.
Complete Elliptic Integral of the First Kind
The complete elliptic integral of the first kind is defined as follows:
\begin{align*} K(x) &= \int_0^{\pi/2}\frac{d\phi}{\sqrt{1-x^2\sin^2\phi}}\\ &= \frac{\pi}{2}\sum_{n=0}^{\infty}\left[\frac{(2n-1)!!}{(2n)!!}\right]^2x^{2n}\\ &= \frac{\pi}{2}\sum_{n=0}^{\infty}\binom{2n}{n}^2\left(\frac{x}{4}\right)^{2n}\\ &= \frac{\pi}{2}\left(1+\frac{x^2}{4}+\frac{9x^4}{64}+\frac{25x^6}{256}+\frac{1225x^8}{16384}+\frac{3969x^{10}}{65536}+\frac{53361x^{12}}{1048576}+\frac{184041x^{14}}{4194304}+\cdots\right) \end{align*}The following approximations are for \(K(x)/(\pi/2)\).
First approximation
\begin{align*} k_1(x) &= \frac{x^2-4}{2x^2-4}\\ &= \frac{1}{2}+\frac{1}{2-x^2}\\ &= 1+\frac{x^2}{4}+\frac{x^4}{8}+\frac{x^6}{16}+\frac{x^8}{32}+\frac{x^{10}}{64}+\frac{x^{12}}{128}+\frac{x^{14}}{256}+\cdots \end{align*}The error is:
\begin{align*} \epsilon_1(x) &= \frac{K(x)}{\pi/2} - k_1(x)\\ &= \frac{x^4}{64}+\frac{9x^6}{256}+\frac{713x^8}{16384}+\frac{2945x^{10}}{65536}+\cdots \end{align*}Second approximation
\begin{align*} k_2(x) &= \frac{3x^4-44x^2+64}{9x^4-60x^2+64}\\ &= \frac{1}{3}+\frac{8}{9(4-3x^2)}+\frac{64}{9(16-3x^2)}\\ &= 1+\frac{x^2}{4}+\frac{9x^4}{64}+\frac{99x^6}{1024}+\frac{1161x^8}{16384}+\frac{13851x^{10}}{262144}+\frac{165969x^{12}}{4194304}+\frac{1990899x^{14}}{67108864}+\cdots \end{align*}The error is:
\begin{align*} \epsilon_2(x) &= \frac{K(x)}{\pi/2} - k_2(x)\\ &= \frac{x^6}{1024}+\frac{x^8}{256}+\frac{2025x^{10}}{262144}+\frac{47475x^{12}}{4194304}+\cdots \end{align*}Third approximation
\begin{align*} k_3(x) &= \frac{x^8-44x^6+432x^4-1280x^2+1024}{4x^8-96x^6+672x^4-1536x^2+1024}\\ &= \frac{1}{4}+\frac{2-x^2}{(4-x^2)^2-8}+\frac{4(4-x^2)}{(8-x^2)^2-32}\\ &= 1+\frac{x^2}{4}+\frac{9x^4}{64}+\frac{25x^6}{256}+\frac{153x^8}{2048}+\frac{493x^{10}}{8192}+\frac{3267x^{12}}{65536}+\frac{10985x^{14}}{262144}+\cdots \end{align*}The error is:
\begin{align*} \epsilon_3(x) &= \frac{K(x)}{\pi/2} - k_3(x)\\ &= \frac{x^8}{16384}+\frac{25x^{10}}{65536}+\frac{1089x^{12}}{1048576}+\frac{8281x^{14}}{4194304}+\cdots \end{align*}Fourth approximation
\begin{align*} k_4(x) &= \frac{25x^{12}-2300x^{10}+50640x^8-403200x^6+1376256x^4-2031616x^2+1048576}{125x^{12}-6500x^{10}+101200x^8-633600x^6+1802240x^4-2293760x^2+1048576}\\ &= \frac{1}{5}+\frac{8(8-5x^2)}{25(5(2-x^2)^2-4)}+\frac{64(32-5x^2)}{25(5(8-x^2)^2-64)}+\frac{128(16-5x^2)}{25(5(16-x^2)^2-1024)}\\ &= 1+\frac{x^2}{4}+\frac{9x^4}{64}+\frac{25x^6}{256}+\frac{1225x^8}{16384}+\frac{15875x^{10}}{262144}+\frac{53325x^{12}}{1048576}+\frac{2936375x^{14}}{67108864}+\cdots \end{align*}The error is:
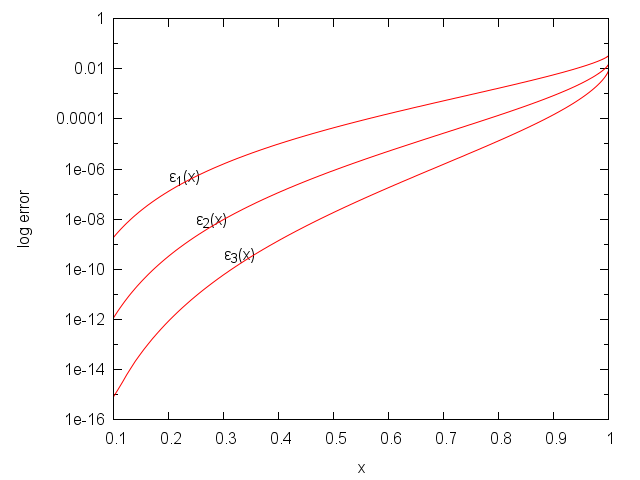
\begin{align*} \epsilon_4(x) &= \frac{K(x)}{\pi/2} - k_4(x)\\ &= \frac{x^{10}}{262144}+\frac{9x^{12}}{262144}+\frac{8281x^{14}}{67108864}+\frac{41095625x^{16}}{1073741824}+\cdots \end{align*}The following is a logarithmic plot of the errors. Below x = 0.1 the errors are too small to calculate accurately.
Complete Elliptic Integral of the Second Kind
The complete elliptic integral of the second kind is defined as follows:
\begin{align*} E(x) &= \int_0^{\pi/2}{\sqrt{1-x^2\sin^2\phi}\;\;d\phi}\\ &= \frac{\pi}{2}\left[1-\sum_{n=1}^{\infty}\left[\frac{(2n-1)!!}{(2n)!!}\right]^2\frac{x^{2n}}{2n-1}\right]\\ &= \frac{\pi}{2}\left[1-\sum_{n=1}^{\infty}\binom{2n}{n}^2\frac{1}{2n-1}\left(\frac{x}{4}\right)^{2n}\right]\\ &= \frac{\pi}{2}\left[1-\frac{x^2}{4}G(x)\right] \end{align*} \begin{equation*} G(x) = \sum_{n=0}^{\infty}\binom{2n}{n}^2\frac{2n+1}{(n+1)^2}\left(\frac{x}{4}\right)^{2n} \end{equation*}The following approximations are for \(G(x)\).
First approximation
\begin{align*} g_1(x) &= \frac{x^4-28x^2+64}{4x^4-40x^2+64}\\ &= \frac{1}{4}+\frac{4}{8-x^2}+\frac{1}{2(2-x^2)}\\ &= 1+\frac{3x^2}{16}+\frac{9x^4}{128}+\frac{33x^6}{1024}+\frac{129x^8}{8192}+\frac{513x^{10}}{65536}+\frac{2049x^{12}}{524288}+\frac{8193x^{14}}{4194304}+\cdots \end{align*}Second approximation
\begin{align*} g_2(x) &= \frac{3x^{10}-336x^8+8512x^6-67072x^4+172032x^2-131072}{18x^{10}-984x^8+16256x^6-93696x^4+196608x^2-131072}\\ &= \frac{1}{6}+\frac{8}{3(16-x^2)}+\frac{64-16x^2}{3(x^2-16)^2-576}+\frac{40}{9(16-3x^2)}+\frac{2}{9(4-3x^2)}\\ &= 1+\frac{3x^2}{16}+\frac{5x^4}{64}+\frac{173x^6}{4096}+\frac{423x^8}{16384}+\frac{17753x^{10}}{1048576}+\frac{6091x^{12}}{524288}+\frac{2206389x^{14}}{268435456}+\cdots \end{align*}Third approximation
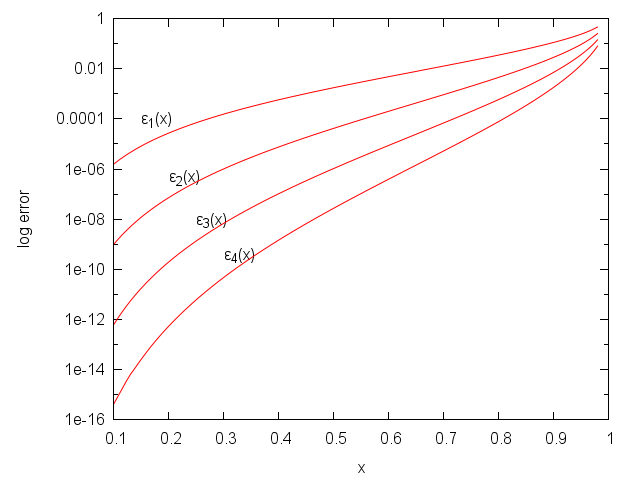
\begin{align*} g_3(x) &= \frac{\begin{array}{l}x^{20}-302x^{18}+28432x^{16}-1175360x^{14}+24196096x^{12}-266125312x^{10}\\+1636958208x^8-5719982080x^6+11106516992x^4-11005853696x^2+4294967296\end{array}}{\begin{array}{l}8x^{20}-1472x^{18}+96576x^{16}-3011584x^{14}+49473536x^{12}-453443584x^{10}\\+2402025472x^8-7415529472x^6+12985565184x^4-11811160064x^2+4294967296\end{array}}\\ &= \frac{1}{8}+\frac{32-4x^2}{x^4-32x^2+128}+\frac{8-2x^2}{x^4-16x^2+32}+\frac{4-3x^2}{4\left(x^4-8x^2+8\right)}\\ &\quad -\frac{x^3-8x^2+32}{2\left(x^4-16x^3+64x^2-128\right)}+\frac{x^3+8x^2-32}{2\left(x^4+16x^3+64x^2-128\right)}\\ &= 1+\frac{3x^2}{16}+\frac{5x^4}{64}+\frac{175x^6}{4096}+\frac{881x^8}{32768}+\frac{9647x^{10}}{524288}+\frac{27885x^{12}}{2097152}+\frac{669451x^{14}}{67108864}+\cdots \end{align*}The following is a logarithmic plot of the errors. Below x = 0.1 the errors are too small to calculate accurately.